2009年普通高等学校招生全国统一考试(江苏卷)
物理试题
一、单项选择题:本题共5小题,每小题3分,共计15分,每小题只有一个选项符合题意。
1.两个分别带有电荷量 ![]()
![]()
![]()
![]()
![]()
A. ![]()
![]()
![]()
![]()
2.用一根长
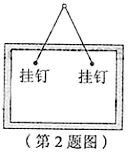
![]()
挂钉的间距最大为( ![]()
![]()
A. ![]()
![]()
C. ![]()
![]()
3.英国《新科学家(New Scientist)》杂志评选出了2008年度世界8项科学之最,在XTEJ1650-500双星系统中发现的最小黑洞位列其中,若某黑洞的半径 ![]()
![]()
![]()
![]()
![]()
![]()
A. ![]()
![]()
C. ![]()
![]()
4.在无风的情况下,跳伞运动员从水平飞行的飞机上跳伞,下落过程中受到空气阻力,下列描绘下落速度的水平分量大小 ![]()
![]()
![]()
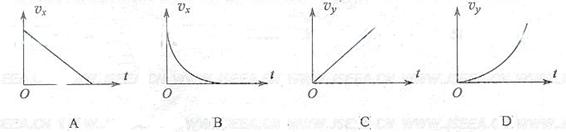
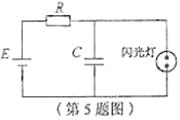
![]()
![]()
![]()
闪光灯周期性短暂闪光,则可以判定
A.电源的电动势 ![]()
![]()
B.电容器所带的最大电荷量一定为![]()
C.闪光灯闪光时,电容器所带的电荷量一定增大
D.在一个闪光周期内,通过电阻 ![]()
荷量一定相等
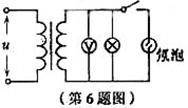
6.如图所示,理想变压器的原、副线圈匝数比为1:5,原线圈两端
的交变电压为 ![]()
时开始发光,下列说法中正确的有
A.开关接通后,氖泡的发光频率为100Hz
B.开关接通后,电压表的示数为100 V
C.开关断开后,电压表的示数变大
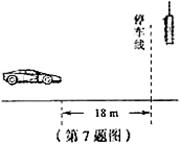
7.如图所示,以 ![]()
还有2 s将熄灭,此时汽车距离停车线
最大加速度大小为 ![]()
![]()
![]()
法中正确的有
A.如果立即做匀加速运动,在绿灯熄灭前汽车可能通过停车线
B.如果立即做匀加速运动,在绿灯熄灭前通过停车线汽车一定超速
C.如果立即做匀减速运动,在绿灯熄灭前汽车一定不能通过停车线
D.如果距停车线 ![]()
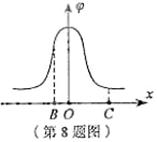
![]()
![]()
![]()
点电场强度在 ![]()
![]()
![]()
A. ![]()
![]()
B. ![]()
![]()
C.电荷在 ![]()
![]()
D.负电荷沿 ![]()
![]()
![]()
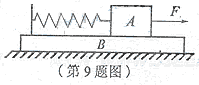
A.当A、B加速度相等时,系统的机械能最大
B.当A、B加速度相等时,A、B的速度差最大
C.当A、B的速度相等时,A的速度达到最大
D.当A、B的速度相等时,弹簧的弹性势能最大
三、简答题:本题分必做题(第10、11题)和选做题(第12题)两部分。攻击42分。请将解答写在答题卡相应的位置。
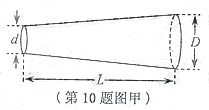
10.(8分)有一根圆台状均匀质合金棒如图甲所示,某同学猜测其电阻的大小与该合金棒的电阻率ρ、长度L和两底面直径d、D有关。他进行了如下实验:
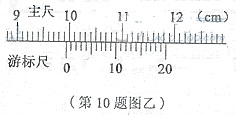
(1)用游标卡尺测量合金棒的两底面直径d、D和长度L。图乙中游标卡尺(游标尺上有20个等分刻度)的读数L=________cm.
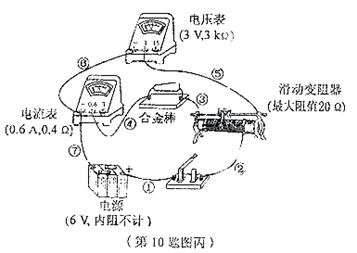
(2)测量该合金棒电阻的实物电路如图丙所示(相关器材的参数已在图中标出)。该合金棒的电阻约为几个欧姆。图中有一处连接不当的导线是__________.(用标注在导线旁的数字表示)
(3)改正电路后,通过实验测得合金棒的电阻R=6.72Ω.根据电阻定律计算电阻率为ρ、长为L、直径分别为d和D的圆柱状合金棒的电阻分别为Rd=13.3Ω、RD=3.38Ω.他发现:在误差允许范围内,电阻R满足R2=Rd·RD,由此推断该圆台状合金棒的电阻R=_______.(用ρ、L、d、D表述)
11.(10分)“探究加速度与物体质量、物体受力的关系”的实验装置如图甲所示.
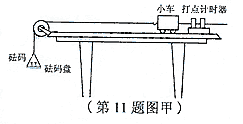

(2)平衡摩擦力后,将5个相同的砝码都放在小车上.挂上砝码盘,然后每次从小车上取一个砝码添加到砝码盘中,测量小车的加速度。小车的加速度a与砝码盘中砝码总重力F的实验数据如下表:
|
砝码盘中砝码总重力F(N) |
0.196 |
0.392 |
0.588 |
0.784 |
0.980 |
|
加速度a(m·s-2) |
0.69 |
1.18 |
1.66 |
2.18 |
2.70 |
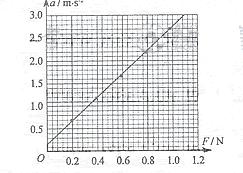
请根据实验数据作出a-F的关系图像.
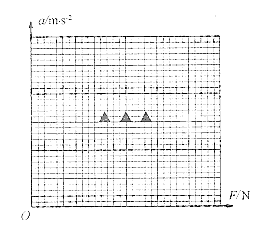
(3)根据提供的试验数据作出的 ![]()
12.[选做题]本题包括 ![]()
![]()
答。若三题都做,则按A、B两题评分
A.(选修模块3—3)(12分)
(1)若一气泡从湖底上升到湖面的过程中温度保持不变,则在此过程中关于气泡中的气体,
下列说法正确的是 ▲ 。(填写选项前的字母)
(A)气体分子间的作用力增大 (B)气体分子的平均速率增大
(C)气体分子的平均动能减小 (D)气体组成的系统地熵增加
(2)若将气泡内的气体视为理想气体,气泡从湖底上升到湖面的过程中,对外界做了0.6J的功,则此过程中的气泡 ▲ (填“吸收”或“放出”)的热量是 ▲ J。气泡到达湖面后,温度上升的过程中,又对外界做了0.1J的功,同时吸收了0.3J的热量,则此过程中,气泡内气体内能增加了 ▲ J
(3)已知气泡内气体的密度为 ![]()
![]()
![]()
B.(选修模块3—4)(12分)
(1)如图甲所示,强强乘电梯速度为0.9 ![]()
![]()
![]()

(A)
(C)

(2)在 ![]()
图乙所示。
质点A振动的周期是租 ▲ s; ![]()
![]()
![]()
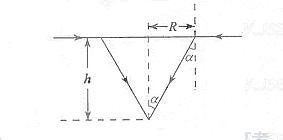
(3)图丙是北京奥运会期间安置在游泳池底部的照相机拍摄的一张照片,照相机的镜头竖直向上。照片中,水利方运动馆的景象呈现在半径 ![]()
![]()
![]()
![]()
C.(选修模块3—5)(12分)
在 ![]()
中微子的性质十分特别,因此在实验中很难探测。1953年,莱尼斯和柯文建造了一个由大水槽和探测器组成的实验系统,利用中微子与水中 ![]()
(1)中微子与水中的 ![]()
![]()
![]()
中微子+ ![]()
![]()
![]()
可以判定,中微子的质量数和电荷数分别是 ▲ 。(填写选项前的字母)
(A)0和0 (B)0和1 (C)1和 0 (D)1和1
(2)上述核反应产生的正电子与水中的电子相遇,与电子形成几乎静止的整体后,可以转变为两个光子( ![]()
![]()
![]()
![]()
![]()
已知正电子和电子的质量都为9.1×10-31㎏,反应中产生的每个光子的能量约为 ▲
J.正电子与电子相遇不可能只转变为一个光子,原因是 ▲ 。
(3)试通过分析比较,具有相同动能的中子和电子的物质波波长的大小。
四、计算题:本题共3小题,共计47分。解答时请写出必要的文字说明、方程式和重要的演算步骤。只写出最后答案的不能得分。有数值计算的题,答案中必须明确写出数值和单位。
13.(15分)航模兴趣小组设计出一架遥控飞行器,其质量m =2㎏,动力系统提供的恒定升力F =28 N。试飞时,飞行器从地面由静止开始竖直上升。设飞行器飞行时所受的阻力大小不变,g取
(1)第一次试飞,飞行器飞行t1 = 8 s 时到达高度H =
(2)第二次试飞,飞行器飞行t2 = 6 s 时遥控器出现故障,飞行器立即失去升力。求飞行器能达到的最大高度h;
(3)为了使飞行器不致坠落到地面,求飞行器从开始下落到恢复升力的最长时间t3 。
14.(16分)1932年,劳伦斯和利文斯设计出了回旋加速器。回旋加速器的工作原理如图所示,置于高真空中的D形金属盒半径为R,两盒间的狭缝很小,带电粒子穿过的时间可以忽略不计。磁感应强度为B的匀强磁场与盒面垂直。A处粒子源产生的粒子,质量为m、电荷量为+q ,在加速器中被加速,加速电压为U。加速过程中不考虑相对论效应和重力作用。
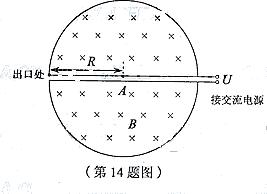
(1) 求粒子第2次和第1次经过两D形盒间狭缝后轨道半径之比;
(2) 求粒子从静止开始加速到出口处所需的时间t ;
(3) 实际使用中,磁感应强度和加速电场频率都有最大值的限制。若某一加速器磁感应强度和加速电场频率的最大值分别为Bm、fm,试讨论粒子能获得的最大动能E㎞。
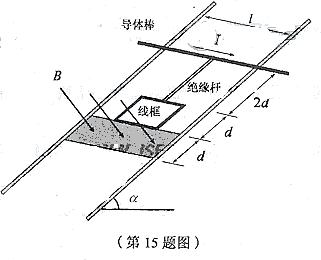
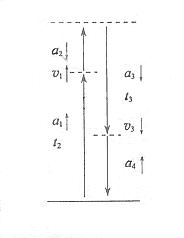
15.(16分)如图所示,两平行的光滑金属导轨安装在一光滑绝缘斜面上,导轨间距为l、
足够长且电阻忽略不计,导轨平面的倾角为 ![]()
![]()
求:(1)装置从释放到开始返回的过程中,线框中产生的焦耳热Q;
(2)线框第一次穿越磁场区域所需的时间t1 ;
(3)经过足够长时间后,线框上边与磁场区域下边界的最大距离 ![]()
物理试题参考答案
一、单项选择题
1.C 2.A 3.C 4.B 5.D
二、多项选择题
三、简答题
10.(1)9.940 (2)⑥ (3)![]()
11.(1)0.16 (0.15也算对)
(2)(见右图)
(3)未计入砝码盘的重力
(3) 设气体体积为 ![]()
![]()
气体分子数 ![]()
![]()
![]()
则 ![]()
![]()
解得 ![]()
![]()
12B.(1)D (2)4 正 10
![]()
![]()
折射定律![]()
几何关系![]()
得![]()
取 ![]()
![]()
![]()
![]()
(3)粒子的动量 ![]()
![]()
由mn>mc,知pn>pc,则![]()
四,计算题
13.(1)第一次飞行中,设加速度为![]()
![]()
由牛顿第二定律![]()
解得![]()
(2)第二次飞行中,设失去升力时的速度为 ![]()
![]()
匀加速运动![]()
设失去升力后的速度为 ![]()
![]()
由牛顿第二定律![]()
![]()
![]()
解得![]()
(3)设失去升力下降阶段加速度为 ![]()
![]()
![]()
由牛顿第二定律 ![]()
F+f-mg=ma4
且![]()
V3=a3t3
解得t3= ![]()
14.(1)设粒子第1次经过狭缝后的半径为r1,速度为v1
qu= ![]()
qv1B=m![]()
解得 ![]()
同理,粒子第2次经过狭缝后的半径 ![]()
则 ![]()
(2)设粒子到出口处被加速了n圈
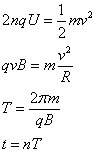
解得 ![]()
(3)加速电场的频率应等于粒子在磁场中做圆周运动的频率,即![]()
当磁场感应强度为Bm时,加速电场的频率应为![]()
粒子的动能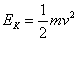
当 ![]()
![]()
![]()
解得![]()
当 ![]()
![]()
![]()
解得 ![]()
15.(1)设装置由静止释放到导体棒运动到磁场下边界的过程中,作用在线框上的安培力做功为W
由动能定理 ![]()
且![]()
解得 ![]()
(2)设线框刚离开磁场下边界时的速度为 ![]()
![]()
由动能定理 ![]()
装置在磁场中运动时收到的合力
![]()
![]()
感应电动势 ![]()
![]()
感应电流 ![]()
![]()
![]()
安培力 ![]()
由牛顿第二定律,在t到t+ ![]()
![]()
则![]()
![]()
有![]()
解得 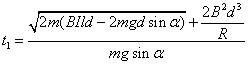
(3)经过足够长时间后,线框在磁场下边界与最大距离 ![]()
由动能定理 ![]()
解得 ![]()






